Wave Nature of Matter

The energy of the electron, in the hydrogen atom, is known to be expressible in the form

$E_n=\frac{-13.6\text{ eV}}{n^2}\left(n=1,2,3,\mathrm{.....}\right).$

sing this expression, which of the following statement is/are true?

(i) Electron in the hydrogen atom cannot have energy of $-6.8\text{ eV}$ .

(ii) Spacing between the lines (consecutive energy levels) within the given set of the observed hydrogen spectrum decreases as n increases.

For what kinetic energy of a proton, will the associated de Broglie wavelength be 16.5 nm?

For what kinetic energy of a neutron the associated de Broglie wavelength be $1.32\times {10}^{-10} \mathrm{m}$?

An $\alpha -$ particle and a proton are accelerated from rest by the same potential. The ratio of their de Broglie wavelengths would be:

An $\alpha -$particle and a proton are accelerated from rest by the same potential. The ratio of their de Broglie wavelengths would be,

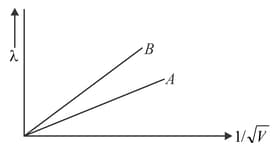
Two lines, A and B, in the plot given below show the variation of de Brogile wavelength,  $\lambda$  versus $1/\sqrt{V}$ , where V is the accelerating potential difference, for two particles carrying the same charge. Which one of two represents a particle of smaller mass?

A proton and an $\alpha$-particle are accelerated from rest by $2 \mathrm{V}$ and $4 \mathrm{V}$ potentials, respectively. The ratio of their de-Broglie wavelength is :

The de Broglie wavelength of an electron having kinetic energy $E$ is $\lambda$. If the kinetic energy of electron becomes $\frac{E}{4}$, then its de-Broglie wavelength will be:

The ratio of the de-Broglie wavelengths of proton and electron having same kinetic energy:
(Assume $m_p=m_e\times 1849$)

Proton $\left(\mathrm{P}\right)$ and electron $\left(\mathrm{e}\right)$ will have same de-Broglie wavelength when the ratio of their momentum is (assume, $m_p=1849$ $m_e$)

The de Broglie wavelength of a molecule in a gas at room temperature $\left(300 \mathrm{K}\right)$ is ${\lambda }_1$. If the temperature of the gas is increased to $600 \mathrm{K}$, then the de Broglie wavelength of the same gas molecule becomes

The kinetic energy of an electron, $\alpha -$particle and a proton are given as $4K, 2K$ and $K$ respectively. The de-Broglie wavelength associated with electron $\left({\lambda }_e\right), \alpha -$particle $\left({\lambda }_{\alpha }\right)$ and the proton $\left({\lambda }_p\right)$ are as follows:

If de-Broglie wavelength is $\lambda$ when energy is $E$ (Kinetic energy). Find the wavelength at $\frac{E}{4}$(Kinetic energy).

Find ratio of de-Broglie wavelength of a proton and an $\alpha -$particle, when accelerated through a potential difference of $2 \mathrm{V}$ and $4 \mathrm{V}$ respectively.

For an electron and a proton$\left(m_p=1847 m_e\right)$ with same de-Broglie wavelength, the ratio of linear momentum is equal to:

Kinetic energy of electron, proton and a particle is given as $K, 2K$ and $4K$ respectively, then which of the following gives the correct order of de-Broglie wavelengths of electron, proton and a particle

Given below are two charged subatomic particles P and Q, that are accelerated through same potential difference $V$.

Here, Masses: $m_P=m_Q$ Charges: $\frac{1}{2}{q}_P=q_Q$

Which of the two sub atomic particles will have longer de Broglie wavelength?

de-Broglie wavelength associated with an electron in the $3^{\text{rd }}$ orbit of ${\mathrm{He}}^{+}$ ion is equal to